روش های شگفت انگیز برای یادگیری مثلثات

روش های شگفت انگیز برای یادگیری مثلثات

دوشنبه 15 اردیبهشت‌ماه سال 1393 ساعت 02:30 ب.ظ

این یادداشت رو سر فرصت تکمیل می کنم . . .

لیست اتحادهای مثلثاتی

روش دایره مثلثاتی

روش شش ضلعی جادویی برای اتحادهای ساده

درباره عدد i و جواب کلی معادله درجه دوم

اثبات فرمول اویلر

روش فرمول اویلر برای جمع زوایا و ...

روش ترکیبی فرمول اویلر و فرمول دوموار برای اتحادهای پیشرفته تر

Magic Hexagon for Trig Identities

This hexagon is a special diagram  to help you remember some Trigonometric Identities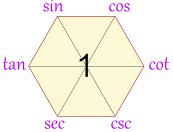

Sketch the diagram when you are struggling with trig identities ... it may help you! Here is how:

Building It: The Quotient Identities

Start with: tan(x) = sin(x) / cos(x) To help you remember think "tsc !"
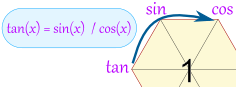Then add: cot (which is cotangent) on the opposite side of the hexagon to tan csc (which is cosecant) next, and sec (which is secant) last
To help you remember: the "co" functions are all on the right

OK, we have now built our hexagon, what do we get out of it?

Well, we can now follow "around the clock" (either direction) to get all the "Quotient Identities":

Clockwise

tan(x) = sin(x) / cos(x) sin(x) = cos(x) / cot(x) cos(x) = cot(x) / csc(x) cot(x) = csc(x) / sec(x) csc(x) = sec(x) / tan(x) sec(x) = tan(x) / sin(x)

Counterclockwise

cos(x) = sin(x) / tan(x) sin(x) = tan(x) / sec(x) tan(x) = sec(x) / csc(x) sec(x) = csc(x) / cot(x) csc(x) = cot(x) / cos(x) cot(x) = cos(x) / sin(x)

Product Identities

The hexagon also shows that a function between any two functions is equal to them multiplied together (if they are opposite each other, then the "1" is between them):

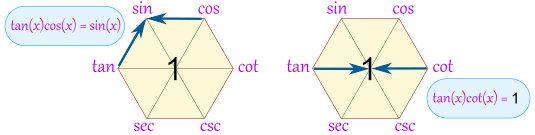Example: tan(x)cos(x) = sin(x)	Example: tan(x)cot(x) = 1

Some more examples:

• sin(x)csc(x) = 1
• tan(x)csc(x) = sec(x)
• sin(x)sec(x) = tan(x)

But Wait, There is More!

You can also get the "Reciprocal Identities", by going "through the 1"

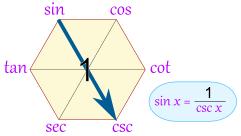Here you can see that sin(x) = 1 / csc(x)

Here is the full set:

• sin(x) = 1 / csc(x)
• cos(x) = 1 / sec(x)
• cot(x) = 1 / tan(x)
• csc(x) = 1 / sin(x)
• sec(x) = 1 / cos(x)
• tan(x) = 1 / cot(x)

Bonus!

AND we also get these:

Examples:

• sin(30°) = cos(60°)
• tan(80°) = cot(10°)
• sec(40°) = csc(50°)

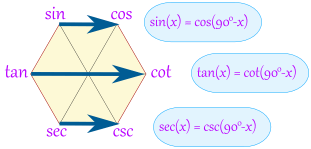
Double Bonus: The Pythagorean Identities

The Unit Circle shows us that

sin² x + cos² x = 1

The magic hexagon can help us remember that, too, by going clockwise around any of these three triangles:

And we have:

• sin²(x) + cos²(x) = 1
• 1 + cot²(x) = csc²(x)
• tan²(x) + 1 = sec²(x)

You can also travel counterclockwise around a triangle, for example:

• 1 - cos²(x) = sin²(x)

Hope this helps you!